排序算法详解

AI-摘要(由百度千帆大模型提供生成摘要能力)
Tianli GPT
AI初始化中...
介绍自己 🙈
生成本文简介 👋
推荐相关文章 📖
前往主页 🏠
前往爱发电购买
排序算法详解
伴随小知识
如何判断一个排序算法是否稳定
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面;
- 不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面;
速记
- 不稳定算法:
快选堆希
排序方式
- In-place(原地算法):指算法执行过程中不需要额外的辅助空间,而是在原始数据上进行操作。
- Out-of-place(非原地算法):指算法执行过程中需要额外的辅助空间来存储数据,而不会在原始数据上进行直接操作。
算法策略
- 分治法:快速排序,归并排序
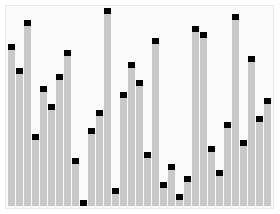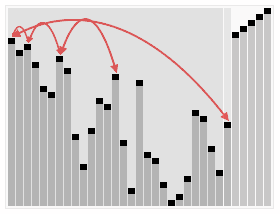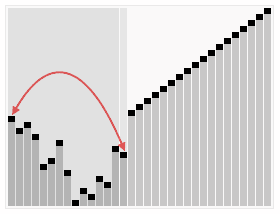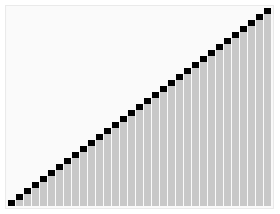
算法详解
基本步骤:
-
比较相邻的两个元素,如果前一个比后一个大(升序排序)或者小(降序排序),则交换它们的位置。
-
对每一对相邻元素重复步骤1,直到列表末尾。这样一次遍历完成后,最大(或最小)的元素将移动到列表末尾。
-
针对剩下的未排序元素重复以上步骤,直到列表中的所有元素都排好序。

基本步骤:
- 遍历数组:从未排序部分找到最小(或最大)的元素。
- 交换位置:将找到的最小(或最大)元素与未排序部分的第一个元素交换位置。
- 缩小范围:将未排序部分的范围缩小一个元素,即将排序范围向右移动一个位置。
- 重复步骤1至步骤3,直到所有元素都被排序完成。

基本步骤:
- 初始状态:将第一个元素视为已排序部分,其余元素视为未排序部分。
- 遍历未排序部分:依次取出未排序部分的元素。
- 插入已排序部分:将取出的元素与已排序部分的元素依次比较,找到合适的位置插入。
- 重复步骤2至步骤3,直到所有元素都被插入到已排序部分。

基本步骤:
- 确定间隔序列:选择一个增量序列(也称为间隔序列),该序列的最后一个元素必须为1。常用的增量序列有希尔建议的序列(例如:{n/2, n/4, …, 1})或者Sedgewick序列。
- 分组排序:根据增量序列,将原始列表分割成若干个子列表,对每个子列表分别进行插入排序。
- 逐步缩小间隔:逐渐缩小增量,重复步骤2,直到增量为1。
- 最后的插入排序:当增量为1时,进行最后一次插入排序,此时列表已经被“预排序”,插入排序的效率较高。

基本步骤:
- 分割:将待排序的列表分成两个子列表,直到每个子列表的长度为1(即列表无法再分割)。
- 排序:对每个子列表进行递归排序。递归的过程就是不断地将列表分割并排序。
- 合并:将两个已排序的子列表合并成一个有序列表。合并过程中,比较两个子列表的头部元素,将较小(或较大)的元素放入合并后的列表中,直到其中一个子列表为空,然后将另一个子列表的剩余部分直接放入合并后的列表中。

基本步骤:
- 选择基准:从列表中选择一个元素作为基准元素(一般情况下是选择数组的第一个或最后一个)。
- 分区:将列表中小于基准元素的元素放在基准元素的左边,大于基准元素的元素放在右边,基准元素放在中间。这个过程称为分区操作。
- 递归排序:对左右两个子列表分别进行递归排序,直到列表为空或只包含一个元素。
- 合并:由于快速排序是原地排序算法,不需要显式的合并步骤。
再详细一点:
- 原数组:[3, 5, 1, 9, 7, 2, 8, 4, 6]
- 选择基准元素 3,分成左半部分 [1, 2] 和右半部分 [5, 9, 7, 8, 4, 6]
- 对左半部分 [1, 2] 递归调用快速排序算法,得到有序数组 [1, 2]
- 对右半部分 [5, 9, 7, 8, 4, 6] 选择基准元素 5,分成左半部分 [4] 和右半部分 [9, 7, 8, 6]
- 对左半部分 [4] 递归调用快速排序算法,得到有序数组 [4]
- 对右半部分 [9, 7, 8, 6] 选择基准元素 9,分成左半部分 [7, 8, 6] 和右半部分 []
- 对左半部分 [7, 8, 6] 选择基准元素 7,分成左半部分 [6] 和右半部分 [8]
- 对左半部分 [6] 递归调用快速排序算法,得到有序数组 [6]
- 对右半部分 [8] 递归调用快速排序算法,得到有序数组 [8]
- 将左半部分 [6]、基准元素 7 和右半部分 [8] 拼接起来,得到有序数组 [6, 7, 8]
- 将左半部分 [4]、基准元素 5 和右半部分 [6, 7, 8, 9] 拼接起来,得到有序数组 [4, 5, 6, 7, 8, 9]
- 将左半部分 [1, 2]、基准元素 3 和右半部分 [4, 5, 6, 7, 8, 9] 拼接起来,得到有序数组 [1, 2, 3, 4, 5, 6, 7, 8, 9]

基本步骤:
- 建立堆:将待排序的列表构建成一个最大堆。这一步通常是从列表的中间位置开始,自底向上地调整每个节点,使得整个列表满足堆的性质。
- 排序:将最大堆中的根节点(即最大值)与堆中的最后一个元素交换位置,并将堆的大小减1。交换后可能会破坏堆的性质,因此需要进行堆调整操作,使得堆重新满足堆的性质。
- 重复步骤2,直到堆的大小为1,此时整个列表已经排序完成。
基本步骤:
- 统计元素出现次数:遍历待排序的列表,统计每个元素出现的次数,并将统计结果存储在一个额外的计数数组中。计数数组的索引对应于待排序元素的值,而数组中的值对应于该元素出现的次数。
- 累加计数:对计数数组进行累加操作,使得每个索引位置的值等于其前面所有索引位置的值之和。这一步可以使得计数数组中的值表示小于等于该索引值的元素个数。
- 输出排序结果:根据计数数组中的统计结果,将待排序列表中的元素放置到正确的位置上,最终得到排序结果。

基本步骤:
- 划分桶:根据待排序元素的范围,确定一定数量的桶,并将待排序元素分配到相应的桶中。
- 桶内排序:对每个桶中的元素进行排序。可以使用任何适合的排序算法,如插入排序、快速排序等。
- 合并结果:按照桶的顺序依次取出各个桶中的元素,即可得到有序的结果。
基本步骤:
- 按位排序:从最低位开始,对待排序的元素按照当前位数进行排序。可以使用稳定的排序算法,如计数排序或桶排序。
- 重复排序:重复第一步的过程,对每一位进行排序,直到对最高位进行排序。
- 合并结果:完成所有位的排序后,即可得到有序的结果。

总结
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n) | O(n) | O(1) | In-place | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | In-place | 不稳定 |
| 插入排序 | O(n^2) | O(n) | O(n^2) | O(1) | In-place | 稳定 |
| 希尔排序 | O(n log n) | O(n log^2 n) | O(n log^2 n) | O(1) | In-place | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n logn) | O(n) | Out-place | 稳定 |
| 快速排序 | O(n log n) | O(n log n) | O(n^2) | O(log n) | In-place | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | In-place | 不稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | Out-place | 稳定 |
| 桶排序 | O(n+k) | O(n+k) | O(n^2) | O(n+k) | Out-place | 稳定 |
| 基数排序 | O(n×k) | O(n×k) | O(n×k) | O(n+k) | Out-place | 稳定 |
评论
匿名评论隐私政策